3D图形编程的数学基础(2)-矩阵及其计算
接上一篇讲向量的文章, 继续讲3D图形编程中的数学中最关键的概念, 矩阵.
目录:
矩阵(matrix)的概念
由m * n 个数有序地排成m行n列的数表, 称为一个m行n列的矩阵, 一般用大写表示. 全零的称为零矩阵.
以下是一个 4 × 3 矩阵: \(\begin{bmatrix} 1 & 2 & 3 \\\\ 1 & 2 & 7 \\\\ 4 & 9 & 2 \\\\ 6 & 1 & 5 \\\\ \end{bmatrix}\)
某矩阵 A 的第 i 行第 j 列, 或 i, j 位, 通常记为 \( A[i , j] \)或 \( A_{i, j} \). 在上述例子中 \( A[2, 3] = 7 \). (来自wikipedia)
当一个矩阵仅包含单行或单列时, 这样的矩阵就称为行向量或列向量. 相关概念可参考上一篇3D 编程的数学基础(1) 向量及其运算 下面演示用 Matlab 生成一个 4*4 的矩阵.
>> A = [ 16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
]
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
实际使用中, 输入矩阵的形式上非常像数学中的矩阵标记方法, 这也是 Matlab 不愧其名的一个地方, 矩阵实验室… 相对来说同类软件 Mathematica 不区分行列, 以类似数组形式来处理矩阵的方法, 更像是通常我们在一般编程语言中的做法, 真从对矩阵的处理直观上来说, 还是不如 Matlab. 虽然在除了这个方面以外的所有方面, 我都更喜欢 Mathematica, 不过这点还是得承认, 并且, 不要小看这一点记法上的区别, 区别可大了去了, 基本可类比 Bash 中对 Shell 命令的处理的直观性和你用 Python, Ruby 去写 Shell 脚本处理一样的感觉. Python, Ruby 再强大, 在大量 Shell 调用的脚本中, 还是远不如 Bash 脚本方便.
下面是 Mathematica 中定义一个矩形的样子, 类似一般语言定义二维数组
In[1]:= A = { {16, 2, 3, 13}, {5, 11, 10, 8}, {9, 7, 6, 12}, {4, 14, 15, 1} }
Out[1]= { {16, 2, 3, 13}, {5, 11, 10, 8}, {9, 7, 6, 12}, {4, 14, 15, 1} }
In[2]:= A // MatrixForm
Out[2]//MatrixForm= 16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
事实上, 在 Irrlicht 与 DirectX 中, 都只有 4*4 的矩阵, 原因以后再讲, 在 Irrlicht 中矩阵用模板类 CMatrix4 表示, 并且有
typedef CMatrix4 matrix4;
DirectX 中的矩阵是用 D3DXMATRIX 表示, 并且功能上设计的比 D3D 中的矩阵会多很多.
在 DirectX 中, 此结构继承自以下结构.
typedef struct _D3DMATRIX {
union {
struct {
float _11, _12, _13, _14;
float _21, _22, _23, _24;
float _31, _32, _33, _34;
float _41, _42, _43, _44;
};
float m[4][4];
};
} D3DMATRIX;
也就是说, 在 DirectX 中以 m[4][4] 的二维数组来表示 4*4 的矩阵. 与 Irrlicht 不同, 在 Irrlicht 中是用 TM[16]; 来表示的. 但是使用上大致相同, 因为都重载了 () 操作符, 可以以 A(i, j) 的方式来获取矩阵 A 的第 i 行, 第 j 列的值.
比如, 我们有一个如下的矩阵.
A =
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
D3D中构造及遍历的代码如下:
#include
#include
int _tmain(int argc, _TCHAR* argv[])
{
D3DXMATRIX A(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16);
for(int i = 0; i < 4; ++i)
{
for(int j = 0; j < 4; ++j)
{
printf("%.2f/t", A(i, j));
}
printf("/n");
}
return 0;
}
结果:
1.00 2.00 3.00 4.00
5.00 6.00 7.00 8.00
9.00 10.00 11.00 12.00
13.00 14.00 15.00 16.00
Irrlicht中:
#include
#include
using namespace irr::core;
int _tmain(int argc, _TCHAR* argv[])
{
matrix4 A;
float m[16] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
A.setM(m);
for(int i = 0; i < 4; ++i)
{
for(int j = 0; j < 4; ++j)
{
printf("%.2f/t", A(i, j));
}
printf("/n");
}
return 0;
}
输出结果一样.
行优先及列优先
这个概念与与数学无关, 仅与计算机存储矩阵的物理方式有关.
在 D3D 及 Irrlicht 中, 顺序的输出矩阵, 是先遍历行, 然后再遍历列, 这种方式叫行优先或者行主序(row-major order), 这里特意提出来是因为事实上还有先遍历列然后遍历行的存储方式, 称为列优先或者列主序(Column-major order). 给大家一个参考资料(Wikipedia的Row-major_order)
D3D中的遍历:(需要强转成FLOAT数组后然后遍历)
for(int i = 0; i < 16; ++i)
{
printf("%.2f/t", ((FLOAT*)A)[i] );
}
Irrlicht中的遍历:
for(int i = 0; i < 16; ++i)
{
printf("%.2f/t", A[i]);
}
假如大家全部用行优先的存储方式, 那么我就不用再多费口舌讲列优先了, 事实上, OpenGL 就采用了列优先的存储方式, 呵呵, 似乎 OpenGL 生来就是与这个世界相反的的, 坐标系 D3D, Irrlicht 用右手坐标系吧, OpenGL 就偏偏用左手坐标系, D3D, Irrlicht 用行优先存储矩阵吧, OpenGL 就偏偏用列优先方式存储矩阵…… 用长沙话来说, 这叫逗霸… 当然, 其实从历史来说, 应该是这个世界与OpenGL唱反调才对.
在 OpenGL 中, 没有为矩阵设计结构, 仅用数组表示, 这也体现了 OpenGL 的底层和原始, 假如用 glLoadMatrix 来加载一个矩阵的话, 此矩阵应该是这样排列的:
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
郁闷了吧……… 别理我, 让我先哭一会儿…
矩阵加减, 数乘
与向量类似, 这里也不多描述了. 也就是对应元素的简单加减乘操作. 概念非常简单, 不多描述了. 看看实际的操作.
>> A = [ 16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
]
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> B = A + A
B =
32 4 6 26
10 22 20 16
18 14 12 24
8 28 30 2
>> C = B - A
C =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> D = A * 2
D =
32 4 6 26
10 22 20 16
18 14 12 24
8 28 30 2
可以看到C = A和D = B = A + A = C * 2, 对应元素的计算, 非常简单. 事实上D3D,Irrlicht中的矩阵类都已经重载了相关的运算符, 直接使用即可.
矩阵的转置(Transpose)
矩阵的转置可通过交换矩阵的行和列来实现. 所以, 一个mn矩阵的转置是一个nm矩阵. 我们用来表示矩阵M的转置.
设A为m ×n阶矩阵(即m行n列), 第i行j列的元素是\(a_{ij}\), 即:\(A=(a_{ij})\)
直观来看, 将A的所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转, 即得到A的转置. 一个矩阵M, 把它的第一行变成第一列, 第二行变成第二列, ……,最末一行变为最末一列, 从而得到一个新的矩阵N. 这一过程称为矩阵的转置.
基本性质
(以下T都是上标) \((A \pm B)^T=A^T \pm B^T\) \((A \times B)^T = B^T \times A^T\) \((A^T)^T = A\)
在MATLAB中, 有现成的转置函数:
>> A = [1 2 3 4]
A =
1 2 3 4
>> transpose(A)
ans =
1
2
3
4
上面也体现了转置最常用的用法, 将行向量转为列向量. 再看个矩阵的例子.
>> E = [1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16]
E =
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
>> transpose(E)
ans =
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
将E的计数增长行列交换了, 假如保持获取元素的下标与上述计数增长一致, 事实上相当于将行优先转化为列优先, 这也是实际中转置的一种用途.
比如在OpenGL中使用列优先, 但是假如我们有的都是行优先数据怎么办?可以通过加载转置矩阵的方式加载, 即
glLoadTransposeMatrix*函数.
在D3D中由函数D3DXMatrixTranspose实现转置.
在Irrlicht中实现转置的代码如下:
// returns transposed matrix
template <class T>
inline CMatrix4<T> CMatrix4<T>::getTransposed() const
{
CMatrix4<T> t ( EM4CONST_NOTHING );
getTransposed ( t );
return t;
}
// returns transposed matrix
template <class T>
inline void CMatrix4<T>::getTransposed( CMatrix4<T>& o ) const
{
o[ 0] = M[ 0];
o[ 1] = M[ 4];
o[ 2] = M[ 8];
o[ 3] = M[12];
o[ 4] = M[ 1];
o[ 5] = M[ 5];
o[ 6] = M[ 9];
o[ 7] = M[13];
o[ 8] = M[ 2];
o[ 9] = M[ 6];
o[10] = M[10];
o[11] = M[14];
o[12] = M[ 3];
o[13] = M[ 7];
o[14] = M[11];
o[15] = M[15];
#if defined ( USE_MATRIX_TEST )
o.definitelyIdentityMatrix=definitelyIdentityMatrix;
#endif
}
理解上应该很简单, 因为转置本身就很简单.
矩阵乘法
矩阵乘法被参考1称为3D图形学中最重要的运算, 没有之一.
它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有定义. 若A为m ×n矩阵, B为n ×p矩阵, 则他们的乘积AB会是一个m ×p矩阵. 其乘积矩阵的元素如下面式子得出:
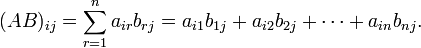
矩阵乘法不符合交换率, 所以将 AB 称为矩阵A右乘B , 或B左乘A.
其实上述的代数方程, 已经一些解释都非常难以理解, 比如”Wikipedia矩阵乘法”上的讲解, 讲了半天, 倒是把我快绕晕了. 我见过最易懂的解释来自于参考1, AB的第ij个元素值等于A的第i个行向量与B的第j个列向量的点积. 点积的概念参考参考上一篇向量的知识, 因为使用了更高一级的名词(更为抽象), 所以更好理解, 比教你怎么去拼, 怎么去记公式要好.
简单的说: \(C_{ij} = A_i \cdot B_j\)
先设定函数dotp以计算行向量A与列向量B之间的点积.
function ret = dotp (A, B)
ret = sum(A .* transpose(B))
end
验证一下我们自己写的函数:
>> A = [1 2 3 4]
A =
1 2 3 4
>> B = [1
5
9
13
]
B =
1
5
9
13
>> dotp(A, B)
ans =
90
此时, 用带上点积的定义实现两个向量的矩阵乘法函数, 如下:
function ret = mul (A, B)
for i = 1 : length(A)
for j = 1 : length(B)
ret(i,j) = dotp(A(i,1:length(A)), B(1:length(B), j))
end
end
endfunction
同样验证一下:
>> E
E =
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
>> F
F =
1 1 1 1
2 2 2 2
3 3 3 3
4 4 4 4
>> M = mul(E, F)
ret =
30
ret =
30 30
ret =
30 30 30
ret =
30 30 30 30
ret =
30 30 30 30
70 0 0 0
ret =
30 30 30 30
70 70 0 0
ret =
30 30 30 30
70 70 70 0
ret =
30 30 30 30
70 70 70 70
ret =
30 30 30 30
70 70 70 70
110 0 0 0
ret =
30 30 30 30
70 70 70 70
110 110 0 0
ret =
30 30 30 30
70 70 70 70
110 110 110 0
ret =
30 30 30 30
70 70 70 70
110 110 110 110
ret =
30 30 30 30
70 70 70 70
110 110 110 110
150 0 0 0
ret =
30 30 30 30
70 70 70 70
110 110 110 110
150 150 0 0
ret =
30 30 30 30
70 70 70 70
110 110 110 110
150 150 150 0
ret =
30 30 30 30
70 70 70 70
110 110 110 110
150 150 150 150
M =
30 30 30 30
70 70 70 70
110 110 110 110
150 150 150 150
>> E * F
ans =
30 30 30 30
70 70 70 70
110 110 110 110
150 150 150 150
每个计算步骤MATLAB都复现了.
这里, 我们用我们高层抽象的定义实现了mul函数, 并且通过验证, 个人感觉, 这样的定义更加容易记忆, 见仁见智, 且当一家之言吧.
不然, 你愿意这样记住公式也行. . . . . 见Irrlicht的矩阵乘法实现:(除了数量的乘法, 没有牵涉进其他概念, 一个一个去对一下, 看看头晕不晕. )
//! multiply by another matrix
// set this matrix to the product of two other matrices
// goal is to reduce stack use and copy
template <class T>
inline CMatrix4<T>& CMatrix4<T>::setbyproduct_nocheck(const CMatrix4<T>& other_a,const CMatrix4<T>& other_b )
{
const T *m1 = other_a.M;
const T *m2 = other_b.M;
M[0] = m1[0]*m2[0] + m1[4]*m2[1] + m1[8]*m2[2] + m1[12]*m2[3];
M[1] = m1[1]*m2[0] + m1[5]*m2[1] + m1[9]*m2[2] + m1[13]*m2[3];
M[2] = m1[2]*m2[0] + m1[6]*m2[1] + m1[10]*m2[2] + m1[14]*m2[3];
M[3] = m1[3]*m2[0] + m1[7]*m2[1] + m1[11]*m2[2] + m1[15]*m2[3];
M[4] = m1[0]*m2[4] + m1[4]*m2[5] + m1[8]*m2[6] + m1[12]*m2[7];
M[5] = m1[1]*m2[4] + m1[5]*m2[5] + m1[9]*m2[6] + m1[13]*m2[7];
M[6] = m1[2]*m2[4] + m1[6]*m2[5] + m1[10]*m2[6] + m1[14]*m2[7];
M[7] = m1[3]*m2[4] + m1[7]*m2[5] + m1[11]*m2[6] + m1[15]*m2[7];
M[8] = m1[0]*m2[8] + m1[4]*m2[9] + m1[8]*m2[10] + m1[12]*m2[11];
M[9] = m1[1]*m2[8] + m1[5]*m2[9] + m1[9]*m2[10] + m1[13]*m2[11];
M[10] = m1[2]*m2[8] + m1[6]*m2[9] + m1[10]*m2[10] + m1[14]*m2[11];
M[11] = m1[3]*m2[8] + m1[7]*m2[9] + m1[11]*m2[10] + m1[15]*m2[11];
M[12] = m1[0]*m2[12] + m1[4]*m2[13] + m1[8]*m2[14] + m1[12]*m2[15];
M[13] = m1[1]*m2[12] + m1[5]*m2[13] + m1[9]*m2[14] + m1[13]*m2[15];
M[14] = m1[2]*m2[12] + m1[6]*m2[13] + m1[10]*m2[14] + m1[14]*m2[15];
M[15] = m1[3]*m2[12] + m1[7]*m2[13] + m1[11]*m2[14] + m1[15]*m2[15];
#if defined ( USE_MATRIX_TEST )
definitelyIdentityMatrix=false;
#endif
return *this;
}
方阵
行数与列数相同的矩阵称为方阵. 比如, 上述44的矩阵其实都是方阵(就如同矩形是长, 宽可以不一样, 正方形边长一样), 并且, 方阵的行数(列数)称为它的阶, 上述44的矩阵可以被称为4阶方阵, 也是3D图形编程中使用的最多的矩阵.
单位矩阵
主对角线上元素为1, 其他元素为0的方阵, 称为单位矩阵. (Identity Matrix)一般以I表示, 单位矩阵在矩阵算法中相当于普通数学运算的1.
一个单位矩阵与某个矩阵相乘, 不改变该矩阵.
在GNU Octave(MATLAB)中, 也有现成的函数可以获取单位矩阵:
>> eye(4)
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
在Irrlicht中, 获取单位矩阵就更简单了, 默认的matrix4类, 就是单位矩阵.
在D3D中通过函数:
D3DXINLINE D3DXMATRIX* D3DXMatrixIdentity
( D3DXMATRIX *pOut )
获取
逆矩阵
设A是数域上的一个n阶方阵, 若在相同数域上存在另一个n阶矩阵B, 使得:AB=BA=I, 则我们称B是A的逆矩阵, 而A则被称为可逆矩阵, 可逆矩阵也被称为非奇异矩阵、非奇异矩阵、满秩矩阵.
- 可逆矩阵一定是方阵
- 一个可逆矩阵的逆矩阵是唯一的
- 两个可逆矩阵的乘积依然可逆
- 可逆矩阵的转置矩阵也可逆
正交矩阵(我数学书上都没有的概念-_-!)
n阶实矩阵 M称为正交矩阵, 如果:M×=I (定义表示“矩阵M的转置矩阵”. )
则下列诸条件是等价的:
- M 是正交矩阵
- M×= I 为单位矩阵
- 是正交矩阵
- M的各行是单位向量且两两正交
- M的各列是单位向量且两两正交
- (Mx,My)=(x,y) x,y∈R
参考资料:
- 《DirectX 9.0 3D游戏开发编程基础》 , (美)Frank D.Luna著, 段菲译, 清华大学出版社
- 《大学数学》湖南大学数学与计量经济学院组编, 高等教育出版社
- 百度百科及wikipedia
其实这些概念都没有什么难的, 大学中的线性代数课程中的基本概念及用D3D, Irrlicht一起来复习一下而已, 下一篇预计讲解矩阵变换, 应该也是最后一篇了.
修改记录
2015年12月, 将原来用 Freemat 及 Ocatave 实现的部分, 改为 Matlab, 原文使用 Live Writer 编写, 新改为 Markdown 格式.
By 九天雁翎
2009年12月08日 | 九天雁翎的博客