3D图形编程的数学基础(1)-向量及其计算
因为大学时在高等数学课程中学习过线性代数相关的内容, 所以学习3D编程的时候这一段事实上是跳过去了, 学习到某些内容的时候觉得很郁闷, (4, 5年没有用了, 难免忘掉)最后常常依靠高级API完成, 但是事实上这些高级API的算法具体实现啥的基本看不懂, 于是还是决定回来好好的将基础部分弄明白, 当然, 首先是数学部分. 为了更好的达到直观的效果, 还有在复杂矩阵运算的时候验证运算结果, 将引入MATLAB的使用. 具体牵涉到计算的时尽量实现DirectX与Irrlicht两个版本, 也会参考部分源代码. (主要用于看看公式用C/C++的实现)基本上, 我希望能以概念的讲解为主, 最好是直观的讲解.
目录:
- 向量
- 左右手坐标系
- 向量的模
- 三维空间中两点的距离
- 向量的规范化
- 向量的加减法, 数乘
- 向量的加法
- 向量的减法
- 数乘向量
- 点积(dot product)又称数量积或内积
- 叉积(cross product): 也称向量积
- 参考资料:
- 修改记录
向量
只用大小就能表示的量叫数量, 比如温度, 质量等. 既需要用大小表示, 同时还要指明方向的量叫向量, 比如位移, 速度等. 几何学中, 我们用有向线段来表示向量. 有两个变量可以确定一个向量,即向量的长度和向量的方向. 量与位置无关, 有相同长度和方向的两个向量是相等的. 在irrlicht中有专门的类vector2d,vector3d分别来表示2维的, 3维的向量. 在DirectX中用于表示向量的是结构D3DXVECTOR2, D3DXVECTOR3,D3DXVECTOR4.
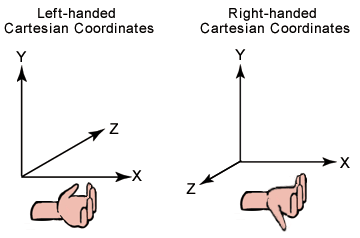
左右手坐标系
一图胜前言, 不懂怎么用手扭曲的去比划的看看图, 就明白啥是左手, 啥是右手坐标系了. 在OpenGL中使用的是右手坐标系, DirectX,Irrlicht中使用的是左手坐标系. (图片来自于网络)
向量的模
向量的大小(或长度)称为向量的模, 向量a的模记为||a||. 下面以3维的向量(3D中用的最多)为例: \(\||a|| = \sqrt{a_x^2 + a_y^2 + a_z^2}\) 在irrlicht中获取向量模的函数是vector3d的成员函数
//! Get length of the vector.
T getLength() const { return core::squareroot( X*X + Y*Y + Z*Z ); }
//! Get squared length of the vector.
/** This is useful because it is much faster than getLength().
/return Squared length of the vector. */
T getLengthSQ() const { return X*X + Y*Y + Z*Z; }
可以看出公式的实现, 其中getLengthSQ用于某些时候使用不开根号, 直接使用平方值的方法来优化代码.
DirectX中的实现差不多一样, 只是使用的是C风格的接口没有使用C++的类而已.
D3DXINLINE FLOAT D3DXVec3Length( CONST D3DXVECTOR3 *pV )
{
#ifdef D3DX_DEBUG
if(!pV)
return 0.0f;
#endif
#ifdef __cplusplus
return sqrtf(pV->x * pV->x + pV->y * pV->y + pV->z * pV->z);
#else
return (FLOAT) sqrt(pV->x * pV->x + pV->y * pV->y + pV->z * pV->z);
#endif
}
D3DXINLINE FLOAT D3DXVec3LengthSq( CONST D3DXVECTOR3 *pV )
{
#ifdef D3DX_DEBUG
if(!pV)
return 0.0f;
#endif
return pV->x * pV->x + pV->y * pV->y + pV->z * pV->z;
}
MATLAB中用norm函数取模:
>> a = [1, 1, 1]
a =
1 1 1
>> b = norm(a)
b =
1.7321
三维空间中两点的距离
公式:
\[\|P_1P_2|=\sqrt{(X_2-X_1)^2+(Y_2-Y_1)^2+(Z_2-Z_1)^2}\]Irrlich的实现:
//! Get distance from another point.
/** Here, the vector is interpreted as point in 3 dimensional space. */
T getDistanceFrom(const vector3d<T>& other) const
{
return vector3d<T>(X - other.X, Y - other.Y, Z - other.Z).getLength();
}
//! Returns squared distance from another point.
/** Here, the vector is interpreted as point in 3 dimensional space. */
T getDistanceFromSQ(const vector3d<T>& other) const
{
return vector3d<T>(X - other.X, Y - other.Y, Z - other.Z).getLengthSQ();
}
也有距离的平方的SQ函数版本.
向量的规范化
向量的规范化也称(归一化)就是使向量的模变为1, 即变为单位向量. 可以通过将向量都除以该向量的模来实现向量的规范化. 规范化后的向量相当于与向量同方向的单位向量, 可以用它表示向量的方向. 由于方向的概念在3D编程中非常重要, 所以此概念也很重要, 单位向量有很多重要的性质, 在表示物体表面的法线向量时用的更是频繁.
基本的公式:
\[\hat{u} = \frac{u}{\||u||} = (\frac{u_x}{\||u||}, \frac{u_y}{\||u||}, \frac{u_z}{\||u||})\]在irrlicht中的调用函数及实现:
//! Normalizes the vector.
/** In case of the 0 vector the result is still 0, otherwise
the length of the vector will be 1.
/return Reference to this vector after normalization. */
vector3d<T>& normalize()
{
f64 length = (f32)(X*X + Y*Y + Z*Z);
if (core::equals(length, 0.0)) // this check isn't an optimization but prevents getting NAN in the sqrt.
return *this;
length = core::reciprocal_squareroot ( (f64) (X*X + Y*Y + Z*Z) );
X = (T)(X * length);
Y = (T)(Y * length);
Z = (T)(Z * length);
return *this;
}
| 上述代码中首先计算length以防其为0, 然后直接计算\( \frac{1}{| | u | } \), (这样做的目的从代码实现上来看是因为SSE,Nviadia都有可以直接计算此值的能力) 然后再分别与各坐标值进行乘法运算. |
DirectX中的API:(无实现可看)
D3DXVECTOR3* WINAPI D3DXVec3Normalize ( D3DXVECTOR3 *pOut, CONST D3DXVECTOR3 *pV );
向量的加减法, 数乘
太简单, 不多描述, 无非就是对应的加, 减, 乘罢了, 几何意义讲一下, 加法可以看做是两个向量综合后的方向, 减法可以看做两个向量的差异方向(甚至可以用于追踪算法), 数乘用于对向量进行缩放.
为了完整, 这里从百度百科拷贝一段资料过来:(以下都是2维的, 放到3维也差不多) 设a=(x, y), b=(x’, y’)
向量的加法
向量的加法满足平行四边形法则和三角形法则.
AB+BC=AC.
a+b=(x+x’, y+y’).
a+0=0+a=a.
向量加法的运算律:
交换律:a+b=b+a;
结合律:(a+b)+c=a+(b+c).
向量的减法
如果a、b是互为相反的向量, 那么a=-b, b=-a, a+b=0. 0的反向量为0
AB-AC=CB. 即“共同起点, 指向被减”
a=(x,y) b=(x’,y’) 则 a-b=(x-x’,y-y’).
数乘向量
实数λ和向量a的乘积是一个向量, 记作λa, 且∣λa∣=∣λ∣·∣a∣.
当λ>0时, λa与a同方向;
当λ<0时, λa与a反方向;
当λ=0时, λa=0, 方向任意.
当a=0时, 对于任意实数λ, 都有λa=0.
注:按定义知, 如果λa=0, 那么λ=0或a=0.
实数λ叫做向量a的系数, 乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.
当∣λ∣>1时, 表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的∣λ∣倍;
当∣λ∣<1时, 表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的∣λ∣倍.
数与向量的乘法满足下面的运算律
结合律:(λa)·b=λ(a·b)=(a·λb).
向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.
数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.
数乘向量的消去律:① 如果实数λ≠0且λa=λb, 那么a=b. ② 如果a≠0且λa=μa, 那么λ=μ.
点积(dot product)又称数量积或内积
公式:
\[a \cdot b = \sum_{i=1}^{n}a_ib_i\]所以向量的点积结果是一个数, 而非向量.
| 点积等于向量v0的长度乘以v1的长度, 再乘以它们之间夹角的余弦, 即 | v0 | * | v1 | *cos(θ). |
通过点积, 可以计算两个向量之间的夹角.
| cos(θ)=v0.v1/ | v0 | v1 | ; |
| θ=Math.acos(v0.v1/ | v0 | v1 | ); |
如果两个向量都是单位向量, 上面的公式可以简化为
θ=Math.acos(v0.v1);
V0.v1=0 =》两个向量互相垂直
V0.v1>0 =》两个向量的夹角小于90度
V0.v1<0 =》两个向量的夹角大于90度
Irrlicht中的实现: (很简单的公式, 很直白的实现)
//! Get the dot product with another vector.
T dotProduct(const vector3d<T>& other) const
{
return X*other.X + Y*other.Y + Z*other.Z;
}
DirectX中的实现:(很简单的公式, 也是很直白的实现)
D3DXINLINE FLOAT D3DXVec3Dot( CONST D3DXVECTOR3 *pV1, CONST D3DXVECTOR3 *pV2 )
{
#ifdef D3DX_DEBUG
if(!pV1 || !pV2)
return 0.0f;
#endif
return pV1->x * pV2->x + pV1->y * pV2->y + pV1->z * pV2->z;
}
叉积(cross product): 也称向量积
叉积的结果是一个向量, 该向量垂直于相乘的两个向量.
公式:
注意:叉积不满足交换律, 反过来相乘得到的向量与原向量方向相反.
左手坐标系可以通过左手法则来确定叉积返回的向量的方向, 从第一个向量向第二个向量弯曲左手, 这是拇指所指的方向就是求得的向量的方向. 右手坐标系同样的, 可以通过右手法则来确定叉积返回的向量的方向, 从第一个向量向第二个向量弯曲右手, 这是拇指所指的方向就是求得的向量的方向. 因此, 事实上叉积获得的向量总是垂直于原来两个向量所在的平面.
如果两个向量方向相同或相反, 叉积结果将是一个零向量. (即a//b)
叉乘的一个重要应用就是求三角形的法向量.
Irrlicht的实现:
//! Calculates the cross product with another vector.
/** /param p Vector to multiply with.
/return Crossproduct of this vector with p. */
vector3d<T> crossProduct(const vector3d<T>& p) const
{
return vector3d<T>(Y * p.Z - Z * p.Y, Z * p.X - X * p.Z, X * p.Y - Y * p.X);
}
DirectX的实现:
D3DXINLINE D3DXVECTOR3* D3DXVec3Cross
( D3DXVECTOR3 *pOut, CONST D3DXVECTOR3 *pV1, CONST D3DXVECTOR3 *pV2 )
{
D3DXVECTOR3 v;
#ifdef D3DX_DEBUG
if(!pOut || !pV1 || !pV2)
return NULL;
#endif
v.x = pV1->y * pV2->z - pV1->z * pV2->y;
v.y = pV1->z * pV2->x - pV1->x * pV2->z;
v.z = pV1->x * pV2->y - pV1->y * pV2->x;
*pOut = v;
return pOut;
}
基本上也就是按公式来了.
MATLAB中叉积用的是cross函数:
>> a = [2,2,1]
a =
2 2 1
>> b= [4,5,3]
b =
4 5 3
>> c = cross(a,b)
c =
1 -2 2
作为最后一个概念, 这里用代码实践一下.
用代码实现上面MATLAB实现的求a=(2,2,1)和b=(4,5,3)的叉积.
Irrlicht版本:
#include <stdio.h>
#include <irrlicht.h>
using namespace irr::core;
int _tmain(int argc, _TCHAR* argv[])
{
vector3df a(2.0f, 2.0f, 1.0f);
vector3df b(4.0f, 5.0f, 3.0f);
vector3df c = a.crossProduct(b);
printf("c = (%f, %f, %f)", c.X, c.Y, c.Z);
return 0;
}
输出:
c = (1.000000, -2.000000, 2.000000)
DirectX版本:
#include <stdio.h>
#include <d3dx9.h>
int _tmain(int argc, _TCHAR* argv[])
{
D3DXVECTOR3 a(2.0f, 2.0f, 1.0f);
D3DXVECTOR3 b(4.0f, 5.0f, 3.0f);
D3DXVECTOR3 c;
D3DXVec3Cross(&c, &a, &b);
printf("c = (%f, %f, %f)", c.x, c.y, c.z);
return 0;
}
输出:
c = (1.000000, -2.000000, 2.000000)
这里给出个较为完整的例子是希望大家了解一下Irrlicht这种C++风格的接口及DirectX的C风格接口使用上的不同, 这里就不对两种风格的接口提出更多评论了, 以防引起口水战.
下一篇预计讲矩阵的计算
参考资料:
- DirectX 9.0 3D游戏开发编程基础, (美)Frank D.Luna著, 段菲译, 清华大学出版社
- 大学数学 湖南大学数学与计量经济学院组编, 高等教育出版社
- 百度百科及wikipedia
修改记录
2015年10月, 将原来用Freemat及Ocatave实现的部分, 改为MATLAB, 原文使用Live Writer编写, 新改为Markdown格式.
By 九天雁翎
2009年12月08日 | 九天雁翎的博客